Introduction
Our first insight into machine learning will be through the simplest model - linear regression. The goal in regression problems is to predict the value of a continuous response variable. First we'll examine linear regression, which models the relationship between a response variable and one explanatory variable. Next, we will discuss polynomial regression and regularization methods.
Simple model
Linear regression tries to minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation. Mathematically it solves a problem of the form:
We'll demonstrate the process using the toy diabetes dataset, included in scikit-learn. For more details about the loading process, take a look at the previous article about loading datasets in Python.
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.cross_validation import train_test_split
# Load the diabetes dataset
diabetes = datasets.load_diabetes()
# Use only one feature
x = diabetes.data[:, np.newaxis]
x_temp = x[:, :, 2]
y = diabetes.target
# Split the data into training/testing sets
x_train, x_test, y_train, y_test = train_test_split(x_temp, y)
# Create linear regression object
model = linear_model.LinearRegression()
# Train the model using the training sets
model.fit(x_train, y_train)
# The coefficients
model.coef_ # array([ 938.23786125])
# The mean square error
np.mean((model.predict(x_test) - y_test) ** 2) # 4017.22
# Explained variance score: 1 is perfect prediction
model.score(x_test, y_test) # 0.31
# Plot outputs
plt.scatter(x_test, y_test, color='black')
plt.plot(x_test, model.predict(x_test), color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
Cross validation
We used the train_test_split function to randomly partition the data into training and test sets. The proportions of the data for both partitions can be specified using keyword arguments. By default, 25 percent of the data is assigned to the test set. Finally, we trained the model and evaluated it on the test set. The resulted r-squared score of 0.31 indicates that 31 percent of the variance in the test set is explained by the model. However the performance might have changed if a different data was chosen as the training set.
To obtain a better understanding of the estimator's performance, we can use cross-validation, whose goal is to define a dataset to "test" the model in the training phase, in order to limit problems like overfitting, and to give an insight on how the model will generalize to an independent dataset.
from sklearn.cross_validation import cross_val_score
...
scores = cross_val_score(model, x_temp, diabetes.target)
scores # array([0.2861453, 0.39028236, 0.33343477])
scores.mean() # 0.3366
cross_val_score by default uses three-fold cross validation, that is, each instance will be randomly assigned to one of the three partitions. Each partition will be used to train and test the model. It returns the value of the estimator's score method for each round. The r-squared scores range from 0.29 to 0.39! The mean of the scores, 0.34, is a better estimate of the estimator's predictive power than the r-squared score produced from a single train/test split.
Polynomial regression
In the previous examples, we assumed that the real relationship between the explanatory variables and the response variable is linear. This assumption is rarely true. Let's discuss polynomial regression, that adds terms with degrees greater than one to the model.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
# function to approximate by polynomial interpolation
def f(x): return x * np.sin(x)
# generate points used to plot
x_plot = np.linspace(0, 10, 100)
# generate points and keep a subset of them
x = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
rng.shuffle(x)
x = np.sort(x[:20])
y = f(x)
# create matrix versions of these arrays
X = x[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]
plt.figure(figsize=(20,10))
plt.plot(x_plot, f(x_plot), label="ground truth")
plt.scatter(x, y, label="training points")
for degree in [1, 3, 5, 8]:
model = make_pipeline(PolynomialFeatures(degree), LinearRegression())
model.fit(X, y)
y_plot = model.predict(X_plot)
plt.plot(x_plot, y_plot, label="degree %d" % degree)
plt.xlim([-0.25,10.25])
plt.ylim([-15.5,9])
plt.legend(loc='lower left')
plt.show()
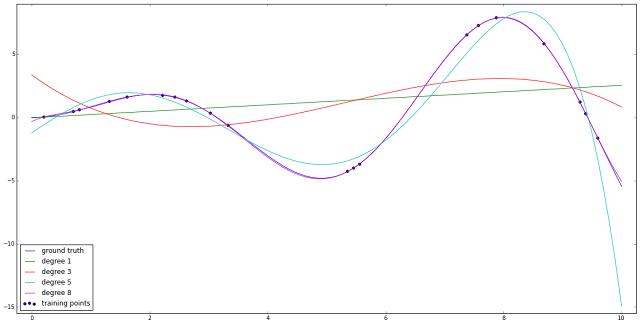
Have a look at the chart above and how different polynomial curves try to estimate the "ground truth" line, colored in blue. The linear green line is no where close to what we seek, but as the degree grows, the curves become more and more close to the one covering all the points - colored in purple.
Regularization
Introduction
In the previous section, one must have felt suspicious of the purple curve covering all the points. And one should be; as the degree of polynomial approximation grows, so does the risk of falling into overfitting. The most common technique to tackle this is regularization.
Regularization is a process of adding the penalty associated with the coefficient values to the error of the hypothesis. This way, an accurate hypothesis with unlikely coefficients would be penalized while a somewhat less accurate but more conservative hypothesis with low coefficients would not be penalized as much.
Two popular regularization methods are L1 and L2, which minimize a loss function E(X, Y) by instead minimizing E(X, Y) + α‖w‖, where w is the model's weight vector, ‖·‖ is either the L1 norm or the squared L2 norm, and α is a free parameter that needs to be tuned empirically. L1 regularization is often preferred because it produces sparse models and thus performs feature selection within the learning algorithm, but since the L1 norm is not differentiable, it may require changes to learning algorithms. L2 penalization is preferable for data that is not at all sparse, i.e. where you do not expect regression coefficients to show a decaying property, which penalizes large weights. In such cases, incorrectly using an L1 penalty for non-sparse data will give you a large estimation error. When applied in linear regression, the resulting models are termed Lasso or Ridge regression respectively.
Implementation
Among other regularization methods, scikit-learn implements both Lasso, L1, and Ridge, L2, inside linear_model package. Let's see the plots after applying each method to the previous code example:
from sklearn.linear_model import Lasso, Ridge
...
for degree in [1, 3, 5, 8]:
model = make_pipeline(PolynomialFeatures(degree), Lasso(alpha = 0.1))
...
from sklearn.linear_model import Lasso, Ridge
...
for degree in [1, 3, 5, 8]:
model = make_pipeline(PolynomialFeatures(degree), Ridge(alpha = 0.1))
...
I've arbitrary chosen the regularization parameter, alpha, to be 0.1, however this may be incorrect and usually more thorough analysis is required. Luckily scikit-learn provides us with methods to do so, an already described cross validation technique to find the best fitting alpha parameter for both Lasso and Ridge methods, called LassoCV and RidgeCV.
from sklearn.linear_model import LassoCV
...
for degree in [1, 3, 5, 8]:
poly = PolynomialFeatures(degree)
X_ = poly.fit_transform(X)
X_plot_ = poly.fit_transform(X_plot)
model = LassoCV(cv=20)
model.fit(X_, y)
print "chosen alpha %d" % model.alpha_
y_plot = model.predict(X_plot_)
plt.plot(x_plot, y_plot, label="degree %d" % degree)
...
# chosen alpha 2
# chosen alpha 265
# chosen alpha 16
# chosen alpha 4783
Notice how all curves got smoothed, in respect to previous results using alpha 0.1 and notice how in each iteration different parameter was chosen.
Conclusion
Now you know how to apply linear regression and different techniques used along with it. In the next article we'll describe logistic regression used in classification problems.
















































